Measuring mesh quality

"Bad quality" elements can, on occasion, cause very poor analytical results. For this reason, the program performs element quality checking to warn user whenever any operation creates an element having a poor shape. Unfortunately, however, there are few universal criteria that can be used to identify a "bad quality" element. In other words, an element that gives poor results in one analysis might give perfectly acceptable results in another analysis. The fact of receiving several element shape warnings does not necessarily mean that element shapes will cause any inaccuracy of results. (Conversely, if any warnings about element shapes are not appearing, that does not guarantee accurate results).

The program evaluates geometric qualities on a subregion of the partition with metrics. A metric is a real number that may be assigned to the subregion. Some metrics, called proper metrics, are normalized so that their values are 1 for ideally-shaped subregions and their values tend to infinite for ill-defined, poor quality, or degenerate subregions.

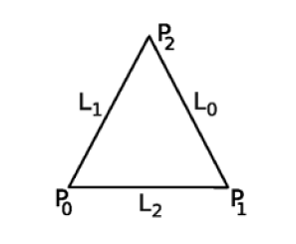
Triangle quality metrics

All the metrics in this section are defined on a triangular element as illustrated in following figure showing the numbering of vertices and edges on a triangular element:

The triangle edge lengths are denoted as follows: L₀, L₁, L₂

And the largest and smallest edge lengths are, respectively:

Lmin = min(L₀, L₁, L₂), Lmax = max(L₀, L₁, L₂)

In addition, we will let r be the in radius (A is the area of the triangle):

and R the circumradius of the triangle:

These are respectively the radii of the inscribed and circumscribed circles of this triangle.

Metric	Description	Dimension	Acceptable Range
Area	Area	L²
Aspect ratio		1
Edge ratio		1
Maximum angle		Angle	°
Minimum angle		Angle	°

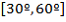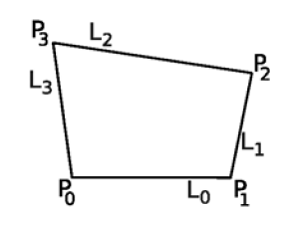
Quadrilateral quality metrics

All the metrics in this section are defined on a quadrilateral element as illustrated in following figure showing the numbering of vertices and edges:

The quadrangle edge lengths are denoted as follows: L₀, L₁, L₂, L₃

And the largest and smallest edge lenghts are, respectively:

Lmin = min(L₀, L₁, L₂, L₃), Lmax = max(L₀, L₁, L₂, L₃)

Metric	Description	Dimension	Acceptable Range
Area	Area	L²
Edge ratio		1
Jacobian	Minimum jacobian computed at each vertex	1
Maximum angle	Maximum included angle of the quadrangle	Angle
Minimum angle	Minimum included angle of the quadrangle	Angle
Warpage	A measure of the deviation out of plane	1

Tetrahedral quality metrics

All the metrics in this section are defined on a tetrahedral element as illustrated in following figure showing the numbering of vertices and edges:

The tetrahedron edge lengths are denoted as follows: L₀, L₁, L₂, L₃, L₄, L₅

And the largest and smallest edge lenghts are, respectively:

Lmin = min(L₀, L₁, L₂, L₃, L₄, L₅), Lmax = max(L₀, L₁, L₂, L₃, L₄, L₅)

The inradius of the tetrahedron is defined as:

where:

V = volume of the tetrahedron,

A = surface area of the tetrahedron.

Metric	Description	Dimension	Acceptable Range
Volume	Volume	L³
Aspect ratio		Dimensionless
Edge ratio		Dimensionless
Jacobian	6 x Volume	Dimensionless
Dihedral angle	Nonoriented dihedral angle of two adjacent faces	Angle	40°- 180°/ ·arccos 1/3
Shape	A measure of the distortion in the shape	Dimensionless

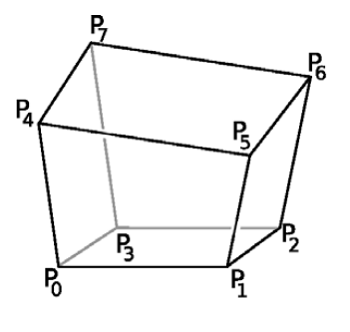
Hexahedral quality metrics

All the metrics in this section are defined on a hexahedral element as illustrated in following figure showing the numbering of vertices and edges:

The tetrahedron edge lengths are denoted as follows: L₀, ... L₁₁

And the largest and smallest edge lenghts are, respectively:

Lmin = min(L₀, ... L₁₁), Lmax = max(L₀, ... L₁₁)

Metric	Description	Dimension	Acceptable Range
Volume	Volume	L³
Edge ratio		Dimensionless	N/A
Jacobian	Minimum determinant of the jacobian matrix evaluated at each vertex and the center of the element	1
Shape	A measure of the distortion in the shape	1